この記事は,
旧ブログ から移植された記事です. よって, その内容として,
旧ブログ に依存した文脈が含まれている可能性があります. 予めご了承下さい.
ベイズの定理の導出から, モンティ・ホール問題への応用まで.
目次
ベイズの定理の導出 モンティ・ホール問題
ベイズの定理の導出
事象 A A A P ( A ) = A P(A) = A P ( A ) = A ÷ \div ÷
事象
B B B のもとで事象
A A A が発生する確率
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) ( P ( B ) > 0 ) P(A\mid B)=\dfrac{P(B\mid A)P(A)}{P(B)}\ (P(B)\gt 0) P ( A ∣ B ) = P ( B ) P ( B ∣ A ) P ( A ) ( P ( B ) > 0 )
と定義される. 以下ベイズの定理を導出する.
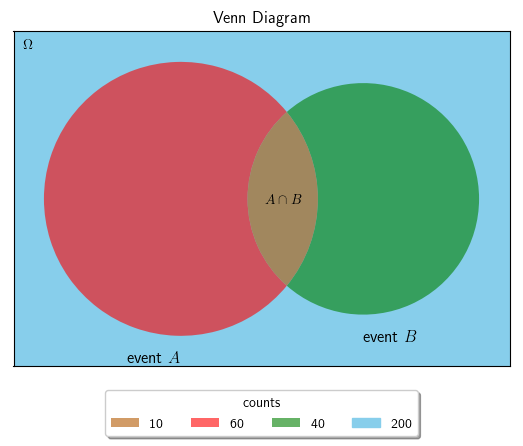
例として, 起こり得る全ての事象の数を 200 200 200 A A A B B B A A A B B B 60 , 40 60,\ 40 60 , 40 A A A B B B 10 10 10
ある事象を表したベン図
まず, A A A B B B P ( A ∩ B ) = P ( B ∩ A ) P(A\cap B) = P(B\cap A) P ( A ∩ B ) = P ( B ∩ A ) A , B A,\ B A , B P ( A ) = 60 200 = 3 10 P ( B ) = 40 200 = 1 5 \begin{array}{lcl}
P(A)&=&\dfrac{60}{200}=\dfrac{3}{10}\\ P(B)&=&\dfrac{40}{200}=\dfrac{1}{5}
\end{array} P ( A ) P ( B ) = = 200 60 = 10 3 200 40 = 5 1 B B B A A A A A A B B B
P ( A ∣ B ) = 10 40 = 1 4 P ( B ∣ A ) = 10 60 = 1 6 \begin{array}{lclcl}
P(A\mid B)&=&\dfrac{10}{40}&=&\dfrac{1}{4}\\
P(B\mid A)&=&\dfrac{10}{60}&=&\dfrac{1}{6}
\end{array}
P ( A ∣ B ) P ( B ∣ A ) = = 40 10 60 10 = = 4 1 6 1
である. そもそも, B B B A A A B B B A A A B B B A A A
P ( A ∩ B ) = P ( A ∣ B ) P ( B ) = 1 4 ⋅ 1 5 = 1 20 P ( B ∩ A ) = P ( B ∣ A ) P ( A ) = 1 6 ⋅ 3 10 = 1 20 \begin{array}{lclclcl}
P(A\cap B)&=&P(A\mid B)P(B)&=&\dfrac{1}{4}\cdot\dfrac{1}{5}&=&\dfrac{1}{20}\\
P(B\cap A)&=&P(B\mid A)P(A)&=&\dfrac{1}{6}\cdot\dfrac{3}{10}&=&\dfrac{1}{20}
\end{array} P ( A ∩ B ) P ( B ∩ A ) = = P ( A ∣ B ) P ( B ) P ( B ∣ A ) P ( A ) = = 4 1 ⋅ 5 1 6 1 ⋅ 10 3 = = 20 1 20 1
である. あとは変形すれば良いだけで,
P ( A ∣ B ) P ( B ) = P ( A ∩ B ) P ( A ∣ B ) = P ( A ∩ B ) P ( B ) P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) \begin{array}{lcl}
P(A\mid B)P(B)&=&P(A\cap B)\\
P(A\mid B)&=&\dfrac{P(A\cap B)}{P(B)}\\
P(A\mid B)&=&\dfrac{P(B\mid A)P(A)}{P(B)}
\end{array} P ( A ∣ B ) P ( B ) P ( A ∣ B ) P ( A ∣ B ) = = = P ( A ∩ B ) P ( B ) P ( A ∩ B ) P ( B ) P ( B ∣ A ) P ( A )
モンティ・ホール問題
確率論的な話となるとよく挙げられる有名な問題, モンティ・ホール問題をベイズの定理で解く.
モンティ・ホール問題とは, 以下の通りである.
(snip)プレーヤーの前に閉まった3つのドアがあって、1つのドアの後ろには景品の新車が、2つのドアの後ろには、はずれを意味するヤギがいる。プレーヤーは新車のドアを当てると新車がもらえる。プレーヤーが1つのドアを選択した後、司会のモンティが残りのドアのうちヤギがいるドアを開けてヤギを見せる。
ここでプレーヤーは、最初に選んだドアを、残っている開けられていないドアに変更してもよいと言われる。プレーヤーはドアを変更すべきだろうか?(snip)ゲームのルール:
3つのドア (A, B, C) に(景品、ヤギ、ヤギ)がランダムに入っている。
プレーヤーはドアを1つ選ぶ。
モンティは残りのドアのうち1つを必ず開ける。
モンティの開けるドアは、必ずヤギの入っているドアである。
モンティはプレーヤーにドアを選びなおしてよいと必ず言う。
– モンティ・ホール問題 - wikipedia
いま, この問題をモンティがヤギのドアを開けた後に,
プレーヤーが景品のドアを開ける条件付き確率問題とし,
プレーヤーが初手で A A A B B B B B B A A A C C C A A A A A A P ( A ∣ B ) P(A\mid B) P ( A ∣ B ) C C C P ( C ∣ B ) P(C\mid B) P ( C ∣ B )
モンティは, プレーヤーが選択した 2 2 2 P ( B ) = 1 2 P(B)=\dfrac{1}{2} P ( B ) = 2 1
プレーヤーが初手で選ぶ段階では, 景品のドアを選ぶ確率は均等であるから, P ( A ) = P ( C ) = 1 3 P(A)=P(C)=\dfrac{1}{3} P ( A ) = P ( C ) = 3 1
これらを基に, まず P ( A ∣ B ) P(A\mid B) P ( A ∣ B )
P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) = 1 2 ⋅ 1 3 1 2 = 1 3
\begin{array}{lclclcl}
P(A\mid B) &=& \dfrac{P(B\mid A)P(A)}{P(B)} &=& \dfrac{\dfrac{1}{2}\cdot\dfrac{1}{3}}{\dfrac{1}{2}}&=&\dfrac{1}{3}
\end{array}
P ( A ∣ B ) = P ( B ) P ( B ∣ A ) P ( A ) = 2 1 2 1 ⋅ 3 1 = 3 1
P ( A ∣ B ) P(A\mid B) P ( A ∣ B ) A A A
A A A B B B C C C P ( B ∣ A ) = 1 2 P(B\mid A)=\dfrac{1}{2} P ( B ∣ A ) = 2 1
から上式のようになる.
次に, P ( C ∣ B ) P(C\mid B) P ( C ∣ B )
P ( C ∣ B ) = P ( B ∣ C ) P ( C ) P ( B ) = 1 ⋅ 1 3 1 2 = 2 3
\begin{array}{lclclcl}
P(C\mid B) &=& \dfrac{P(B\mid C)P(C)}{P(B)}&=&\dfrac{1\cdot \dfrac{1}{3}}{\dfrac{1}{2}}&=&\dfrac{2}{3}
\end{array}
P ( C ∣ B ) = P ( B ) P ( B ∣ C ) P ( C ) = 2 1 1 ⋅ 3 1 = 3 2
P ( C ∣ B ) P(C\mid B) P ( C ∣ B ) C C C
C C C B B B P ( B ∣ C ) = 1 P(B\mid C)=1 P ( B ∣ C ) = 1
から上式のようになる.
よって, ドアの選択を変えるべきであるという解が導かれる.
Wikipedia にも似たような図があるが,
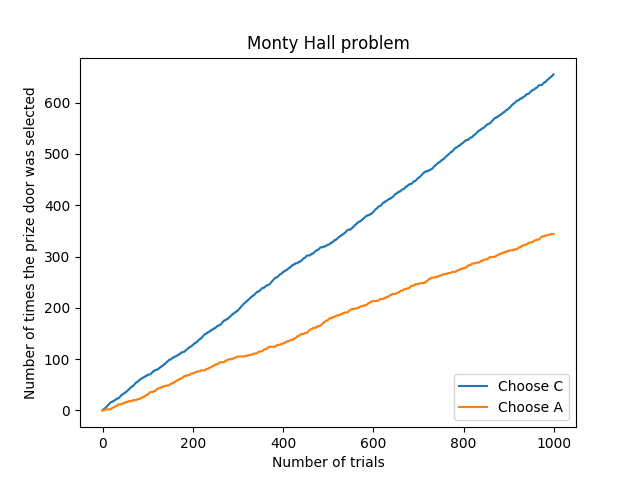
折角なので, 1000 1000 1000
モンティ・ホール問題の視覚化
当たり前ではあるのだが, この図からも,
C C C