エルミート曲線
- 2018/04/16 01:50
-
典型的なパラメトリック曲線の一種である, エルミート曲線についてのメモ.
パラメトリック曲線
そもそもパラメトリック曲線とは, 任意のパラメータから各々の座標を陽関数形式で表現できる曲線のことをいう. このとき定義できる関数 がパラメータ 1 の多項式である場合, それを多項式曲線といい, 有理式である場合, それを有理曲線という. 例えば, 直線の方程式 は,
とパラメタライズできる. この方程式では, パラメタライズせずとも, に 1 つの実数を代入すれば, 必ず が求まる(逆も言える)ことは明らかである. 次に, 3 次曲線 について考える. に 1 つの実数を代入すると, は,
- のとき ,
- のとき ,
- のとき複素数
となり, の値によっては, グラフが存在しない. これを
とパラメタライズすることで, 任意の実数 に対するグラフ上の一点を定めることができる2.
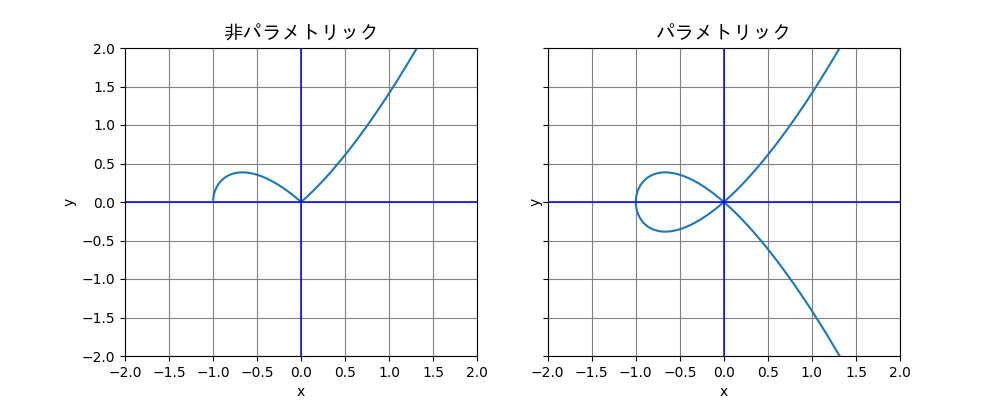
エルミート曲線
エルミート曲線は, 始点 とその速度ベクトル , 終点 とその速度ベクトル を与えたときに, 始点と終点の間をつなぐ 3 次パラメトリック曲線である. 3 次パラメトリック曲線と言うからには, これを一般の 3 次多項式で表現できるはずである. パラメトリック曲線は と をそれぞれ別々に扱えるので, まず について考える. 4 つの係数, が得られれば, 任意の に対するエルミート曲線の が得られるはずである. まず, 始点の座標を求める. のときを始点, のときを終点としたとき, のときに始点の座標, のときに終点の座標が得られることは明らかなので, に , および に を代入して次の二式が得られる. ここで, ある地点 での曲線の傾きを求めるために, 一階微分した次の式を得る. 始点 () と終点 () をそれぞれ式 の に代入し, 始点における曲線の傾きと, 終点における曲線の傾きが得られる.
式 に式 , を, 式 に式 を代入すると, 次の二式が得られる.
式 , の連立方程式を解くと,
となる. 式 を式 に代入すると であるから, 式 から に対するエルミート曲線の が取れることがわかった. についても, を に, を にすると, 同様にして得られるから
がいえる.
さらに, から ( についても同様) の係数にそれぞれ着目して, 次のように定義する.
- の係数に着目し, , これを とする
- の係数に着目し, , これを とする
- の係数に着目し, , これを とする
- の係数に着目し, , これを とする
すると, 先ほど導出した の式は次のように定義できる.
エルミート曲線
これは, 3 次エルミート多項式によるエルミート曲線の定義と同義である.
実際に描く
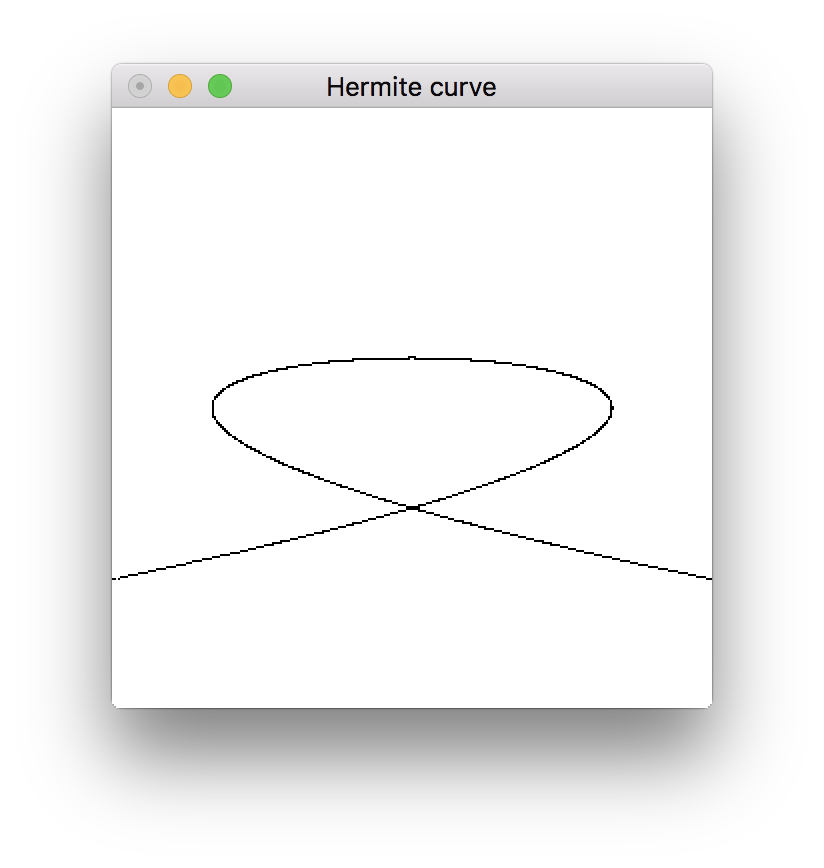
始点 での速度ベクトルを , 終点 での速度ベクトルを として, 上記に導いたエルミート曲線に従い, 点を打ってみた3.
{-# OPTIONS_GHC -Wall #-}
module Main where
import Graphics.Rendering.OpenGL
import Graphics.UI.GLUT
import Control.Monad (forM_)
import Control.Arrow ((&&&))
type Float' = GLfloat
linspaceWithDensity :: Float' -> Int -> Int -> [Float']
linspaceWithDensity density bt et = let distance = round (realToFrac (abs et + abs bt) / density) in
take distance $ iterate (+density) (realToFrac bt :: Float')
-- | The function that generates a coordinate list of Hermite curve according to
--
-- the start point, the velocity vector of the start point, the end point, the velocity vector of the end point,
-- the density of the points and the range of @t@ (@bt <= t <= et@).
hermite :: (Float', Float') -> (Float', Float') -> (Float', Float') -> (Float', Float') -> Float' -> Int -> Int -> [(Float', Float')]
hermite st stVec ed edVec = ((map (herX &&& herY).).).linspaceWithDensity
where
h30 t = (2 * t + 1) * (1 - t)^2
h31 t = t * (1 - t)^2
h32 t = -t^2 * (1 - t)
h33 t = t^2 * (3 - 2 * t)
hermite' t v1 v2 v3 v4 = h30 t * v1 + h31 t * v2 + h32 t * v3 + h33 t * v4
herX t = hermite' t (fst st) (fst stVec) (fst edVec) (fst ed)
herY t = hermite' t (snd st) (snd stVec) (snd edVec) (snd ed)
resize :: Size -> IO ()
resize s@(Size w h) = do
viewport $= (Position 0 0, s)
loadIdentity
ortho (-w') w' (-h') h' (-1.0) 1.0
where
w' = realToFrac w / 200.0
h' = realToFrac h / 200.0
disp :: IO ()
disp = do
clear [ColorBuffer]
color (Color3 0 0 0 :: Color3 GLdouble)
pointSize $= 1.0
renderPrimitive Points $ forM_ hcurve (vertex.(uncurry Vertex2))
flush
where
hcurve = hermite (1, 0) (0, 1) (-1, 0) (0, -1) 0.001 (-2) 2
main :: IO ()
main = do
(progname, _) <- getArgsAndInitialize
initialDisplayMode $= [RGBAMode]
_ <- createWindow progname
clearColor $= Color4 1 1 1 1
windowTitle $= "Hermite curve"
displayCallback $= disp
reshapeCallback $= Just resize
mainLoop次の曲線を得た.
活動継続のためのご支援を募集しています