以前のエントリ¹では, AWS の API を golang から叩くために golang の言語機能を一通り触った. 自分は元々よく C++ を書いていたので golang で叩く前にまず C++ から適当に叩いてみていたのだが, ふと Haskell 用の AWS のライブラリの存在を知り, ひとまず触ってみたので, 記録と紹介を兼ねて書き残してみる. 執筆時現時点では, 公式が提供する AWS SDK は awscli を除き C++, Go, Java, javascript, .NET, PHP, Python, Ruby ²となっており, amazonka³ は非公式の Haskell 用 AWS SDK である. 基本的には, まず amazonka を導入した後, 必要となる AWS サービスに該当する amazonka-** を導入する. 今回は, ec2 インスタンスの立ち上げ, 停止を行なったので, amazonka-ec2⁴ を利用した. amazonka は全体のデータのやり取りに Lens を多様しており, 利用者はこの恩恵を傍受できる.

早速であるが, くだらないサンプルを次に示す. とくにいま ec2 インスタンス上で何かしたいことはないので, 東京リージョンでインスタンスを立ち上げて, その直後に落とすこととする⁵.

module Main where
import qualified Network.AWS as AWS
import qualified Network.AWS.Data as AWSD
import qualified Network.AWS.EC2 as EC2
import System.IO (stdout)
import Control.Lens

instanceIds :: String
instanceIds = "i-********"

main :: IO ()
main = do
    let t0 = EC2.startInstances & EC2.sInstanceIds .~ [AWSD.toText instanceIds]
    let t1 = EC2.stopInstances & EC2.siInstanceIds .~ [AWSD.toText instanceIds]
    env <- AWS.newEnv (AWS.FromFile (AWSD.toText "default") "/path/to/credentials")
    lgr <- AWS.newLogger AWS.Debug stdout
    res0 <- AWS.runResourceT $ AWS.runAWS (env & AWS.envLogger .~ lgr) $ AWS.within AWS.Tokyo $ AWS.send t0
    res1 <- AWS.runResourceT $ AWS.runAWS (env & AWS.envLogger .~ lgr) $ AWS.within AWS.Tokyo $ AWS.send t1
    print res0
    print res1

本家の各 SDK と同じように, 必要なサービスごとにライブラリがそれぞれ独立しているので, 基本的にまずは AWS CLI Command Reference をみてから, その操作を行うのに必要とするライブラリを amazonka から選んで導入することで, 実際に動くまでを円滑に進めることができるだろう.

参照

• “amazonka: Comprehensive Amazon Web Services SDK.” http://hackage.Haskell.org/package/amazonka 2018 年 6 月 24 日アクセス.
• “amazonka-ec2: Amazon Elastic Compute Cloud SDK.” http://hackage.Haskell.org/package/amazonka-ec2-1.6.0 2018 年 6 月 24 日アクセス.
• “Network.AWS” http://hackage.Haskell.org/package/amazonka-1.6.0/docs/Network-AWS.html 2018 年 6 月 24 日アクセス
• “Network.AWS.EC2” http://hackage.Haskell.org/package/amazonka-ec2-1.6.0/docs/Network-AWS-EC2.html 2018 年 6 月 24 日アクセス

大学のレポート内で De Bruijn Sequence について書く機会があった. これまた以前と同じく, 折角なのでこちらのブログにも, 若干内容を変えつつ載せておくことにした.

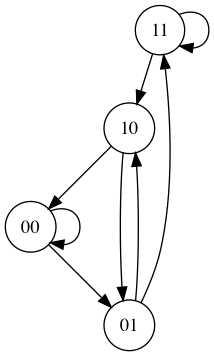
De Bruijn Sequence は, オランダ人の数学者 Nicolaas de Bruijn に因んで命名された系列で, 特定の長さのすべての組み合わせを含む系列である. 次数 $n$ の $k$ 種類に関する De Bruijn Sequence $B(k, n)$ は, 長さ $n$ で表現可能なすべての部分列によって構成される. 次元数 $2$ (すなわちバイナリ) の De Bruijn Sequence は $B(2, n)$ であり, $n$ ビットの固有な部分系列から成る $2^n$ ビット長の系列である. 例えば, $B(2, 3)$ は $00011101_{(2)}$ であり $n$ に対する有向グラフが下図¹のように示される.

フィボナッチ数列を以下の漸化式で定義する.

ここで, 初項と第二項をそれぞれ $a_1=1, a_2=1$ とする. 各項を $f_{n+2}\rightarrow c^2、f_{n+1}\rightarrow c、f_n\rightarrow 1$ と置き換えると $$c^2=c+1\tag{1}$$ が得られる. この解は $c=\dfrac{1\pm{\sqrt{5}}}{2}$ となる. ここで, $\psi = \dfrac{1-\sqrt{5}}{2}, \phi = \dfrac{1+\sqrt{5}}{2}$ と置く. フィボナッチ数列の漸化式の特性方程式の解は $(1)$ の解より $\psi, \phi$ であるから $$f_{n+2}=f_{n+1}+f_{n}\Leftrightarrow\begin{cases}f_{n+2}-\psi f_{n+1}=\phi(f_{n+1}-\psi f_n) \\ f_{n+2}-\phi f_{n+1}=\psi(f_{n+1}-\phi f_n)\end{cases}$$ と変形できる. いま $b_n=f_{n+1}-\psi f_n, c_n=f_{n+1}-\phi f_n$ と置くと次の漸化式が得られる.

典型的なパラメトリック曲線の一種である, ベジェ曲線(Bézier curve)についての学習メモ. パラメトリック曲線とその一種であるエルミート曲線に関しては, 前回の記事を参照.

ベジェ曲線は, パラメータ $t\\ (0 \leq t \leq 1)$ と複数の制御点 $P_i$ から構成されるパラメトリック曲線の一種である¹. 始点と終点の線分から成る, 次数 $n$ のベジェ曲線は $n+1$ の制御点をもち ($= P_0, P_1, \cdots, P_n$ の制御点があるベジェ曲線を $n-1$ 次ベジェ曲線という), この内分点を繰り返し取ることによって, 曲線を得ることができる. この始点と終点の線分を, セグメントといい, これが得られる曲線そのものになる². まず, ここでは 2 次ベジェ曲線を描くとして, そのイメージをつけるために, 図³を用いてその概要を見る. なお, 2 次ベジェ曲線は true type フォントなどで使われている.

典型的なパラメトリック曲線の一種である, エルミート曲線についてのメモ.

パラメトリック曲線

そもそもパラメトリック曲線とは, 任意のパラメータから各々の座標を陽関数形式で表現できる曲線のことをいう. このとき定義できる関数 $f$ がパラメータ $t$¹ の多項式である場合, それを多項式曲線といい, 有理式である場合, それを有理曲線という. 例えば, 直線の方程式 $y = m(x-a)+b$ は,

$$\begin{cases} x=t \\ y=m(t-a)+b \end{cases}$$

とパラメタライズできる. この方程式では, パラメタライズせずとも, $x$ に 1 つの実数を代入すれば, 必ず $y$ が求まる(逆も言える)ことは明らかである. 次に, 3 次曲線 $y^{2} = x^{3} + x^{2}$ について考える.