ベイズの定理の導出から, モンティ・ホール問題への応用まで.

目次

1. ベイズの定理の導出
2. モンティ・ホール問題

以前の記事, エルガマル暗号では, エルガマル暗号に関する諸々の前提の説明と, その実装について示した. 同エントリ内で, フェルマーの小定理¹については取り扱ったものの, その一般形であるオイラーの定理およびカーマイケルの定理について特に触れなかったため, 本エントリでそれらに関してまとめる. しばしば値の確認には, 簡単のため Haskell を使う.

目次

1. オイラーの定理
2. ラグランジュの定理
3. カーマイケルの定理

エルガマル暗号が離散対数問題の応用であることは認知していたものの, きっちりと自分でまとめたことが無かったと思うので, それに関連する諸々の前提についてもふまえて, 一度書くことにした. また, その処理系を実装した. 本エントリでは, 同暗号プロトコルの話の前にまず前提を示し, その後, 実装の観点から見た要点を示す.

目次

1. ユークリッドの互除法
2. ガロア体
3. オイラーの $\phi$ 関数
4. フェルマーの小定理
5. 原始元
6. 離散対数問題
7. 実装
   1. フェルマーテスト, Miller-Rabin 素数判定法
   2. 原始根の生成
   3. 鍵と暗号文の生成
   4. 暗号文の復号
   5. 実行
8. 参考文献

数論的関数の用語やその関連について整理したかったので書くことにした.

目次

1. 数論的関数
   1. 加法的関数
   2. 乗法的関数
2. 参考文献

大学のレポート内で De Bruijn Sequence について書く機会があった. これまた以前と同じく, 折角なのでこちらのブログにも, 若干内容を変えつつ載せておくことにした.

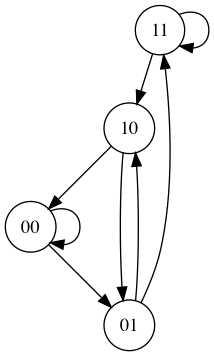
De Bruijn Sequence は, オランダ人の数学者 Nicolaas de Bruijn に因んで命名された系列で, 特定の長さのすべての組み合わせを含む系列である. 次数 $n$ の $k$ 種類に関する De Bruijn Sequence $B(k, n)$ は, 長さ $n$ で表現可能なすべての部分列によって構成される. 次元数 $2$ (すなわちバイナリ) の De Bruijn Sequence は $B(2, n)$ であり, $n$ ビットの固有な部分系列から成る $2^n$ ビット長の系列である. 例えば, $B(2, 3)$ は $00011101_{(2)}$ であり $n$ に対する有向グラフが下図¹のように示される.